Using Single-digit Doubles to Add
This Problem String is designed to develop the strategy of Using Doubles to Add. Grades K-2.
Experience the Problem String
This is a clip of Kim Montague working with first grade students who live near Austin, Texas. These students have had no prior experience with Problem Strings and limited experience with number racks. Kim is a guest teacher.
This clip includes a short introduction to the math rack (rekenrek).
About the Problem String
About the Mathematics and Structure
This Problem String has 5 problems that have the potential to suggest using doubles to find near doubles. This is a relatively short Problem String that makes use of something students may “just know”— doubles—to solve problems that may be less familiar. The first three problems make use of the double 7 + 7. Once the sum of fourteen is established, students can use what they know to solve the second problem, 7 + 6 by considering (7 + 7) − 1.
Similarly, the third problem, 7 + 8, can be seen as (7 + 7) + 1. Both 7 + 6 and 7 + 8 are known as commonly miscalculated problems but when students make use of the associative property, they use relationships they own. The fourth problem in the string presents another double students may already know, 8 + 8. (If not known students can also make use of the double 7+7, by using the third problem, 7 + 8, or using the 10 + 6). The final problem, 8+9, is another commonly missed problem, but can be solved by thinking about (8 + 8) + 1.
The structure of the number rack allows that students could view doubles like 7 + 7 = (5 + 5) + (2 + 2) = 10 + 4 = 14 and 8 + 8 as (5 + 5) + (3 + 3) = 10 + 6. You would probably want to do work on these relationships before doing this Problem String.
The use of the associative property can look like the following equations. This notation is not for students at these ages, but we show it here for teachers’ understanding of the properties underpinning the work.
7 + 6 = (1 + 6) + 6 = 1 + (6 + 6) = 1 + 12 = 13 or 7 + 6 = 7 + (7 − 1) = (7 + 7) − 1 = 14 − 1 = 13
7 + 8 = 7 + (7 + 1) = (7 + 7) + 1 = 14 + 1 = 15 or 7 + 8 = (8 − 1) + 8 = (8 + 8) − 1 = 16 − 1 = 15
8 + 9 = 8 + (8 + 1) = (8 + 8) + 1 = 16 + 1 = 17 or 8 + 9 = (9 − 1) + 9 = (9 + 9) − 1 = 18 − 1 = 17
To Facilitate the String
As you prepare to lead your class through this Problem String, consider the following sample language, strategies to pull out from students, and ideas to highlight:
Facilitate as a quick image by showing for a couple of seconds, covering, showing again. What did you see? How many did you see? Represent strategies with equations.
Repeat for each question.
For each problem after the first, elicit the strategy of using the doubles to help.
So, you can use what you know to solve other problems you don't know. Great!
Important Questions
Consider what you could ask at key times in the Problem String to help students build models, strategies, and big ideas:
How many do you see? How did you see it?
How could you use one the problem before to help you?
How could you use doubles to help you?
General Teacher Moves Common to Most Problem Strings
How is the Problem String facilitated?
Problem Strings are facilitated by the teacher by asking each problem, one at a time. Students work to solve the problem, the teacher calls on individuals to share, and the teacher models (represents) student thinking on the number rack by moving beads and with equations on the display.


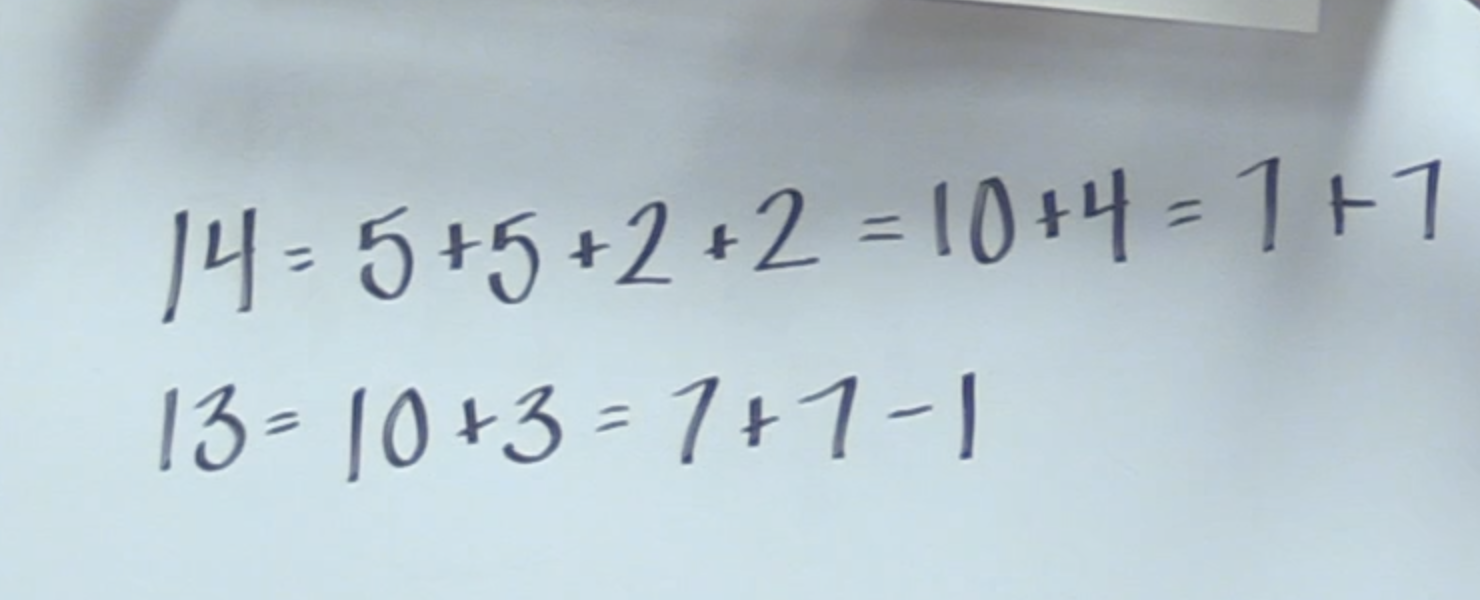
How does the teacher know who to call on?
Since the teacher cannot see who is using the desired strategy, the teacher can ask a question that draws out that strategy, like "Did anyone use the double in the problem before to help?" How do students indicate they are ready? The teacher models and requests a private response signal. Students using a private response signal allows their peers enough work time, is not distracting other students, and gives the teacher valuable information about who is done and who needs more time. In the video, Kim verbally requested a private signal, "Give me a thumbs up. Right here at your chest, when you have something that you can share," and she physically demonstrated the signal by holding her thumb up as she asked questions.
Novice Facilitator Moves Unique to this Problem String
This Problem Strings is facilitated in a "quick image" format. How? Why?
In a Problem String that is facilitated using a "quick image" format, the teacher covers up the number rack, moves the beads to the appropriate places to represent the problem, then removes the cover briefly. The teacher recovers the number rack and pauses, allowing the students to create a mental image in their minds. Then the teacher asks students to share how many they saw and how they know. Sometimes, the teacher may flash the image twice before asking students. The reasons to use a "quick image" format for this Problem String are to help students learn to form mental images that they can refer to and also because students only have a short time to figure out how many beads are shown, they are nudged to use relationships instead of counting one by one. Rather than take the time to count each bead, students seek to figure out how many they see by using the color and 5 and 10 structure of the number rack.
How many strategies does a teacher ask for/represent for each problem during the string?
This Problem String is a strategy building string—its purpose is to build the strategy of using doubles to find the sum of near doubles. Usually in strategy building Problem Strings, teachers ask for and represent fewer alternative strategies. Because these students had little experience with number racks, Kim chose to ask for a few strategies for each problem, but by the end of the Problem String, she had narrowed to focusing on using doubles to find the sum of near doubles.
Fine-grained and Nuanced Teacher Moves
How did Kim build a culture of thinking and reasoning rather than counting one-by-one or rote memorizing a fact?
Questions like, "How do you know?" instead of "What is the answer?" can help students relax into thinking instead of worrying only about answer getting.
The rest of these quotes each have elements of suggesting that math is more about reasoning and communicating justifications and less about answer getting or mimicking procedures:
How did you see those?
Did anyone see that in a different way?
What's the 10, Sofia? Can you see here what Sofia just said? And see what she saw also?
Syndey, what did you see?
Thumbs up if you think you know.
Who heard how Gemma just solved that?
What did you see? And how do you know?
Did anyone use this problem right here that we had just done? Charlotte, you did? Can you talk to me about that?
How did Kim choose who to call on? How do you know which student to choose because you don't know what strategy they are using?
Near the beginning of the Problem String, Kim asks random students how many they see and how they know. As the Problem String progresses, she is looking to find someone who used the 7 + 7 = 14 to help them find the 6 + 7. Notice how she interacts with students to pull out that strategy:
Kim: Sydney, what did you see?
Sydney: 13.
Kim: You saw 13, and how did you see those 13?
Sydney: Cause I saw 10 red and 3 blues.
Kim: Three, how many? Three whites?
Sydney: Yes.
Kim: You saw that as 13. And you saw 10 red and 3 white. Did anyone see 10 and 3? Nice, did anyone see it in a different way? Give me a thumbs up right here. Saw it a different way. Brady, I thought I heard you start to say something. You said it's just ...?
Brady: One less.
Kim: One less than what?
Brady: 14.
Kim: We just had seven and seven. Which was, 14. And you said, it's just one less. So I could also say that 13 is the same as 7 plus 7 minus that 1, nice.
Student: Whoa!
Kim: Really cool...
Kim: restates the doubles relationship because she knows not many of the students were using it. And ending with "real cool," gives students the idea that she is interested in their thinking, especially when they are using relationships. Here is another example:
Kim: You saw 15? Did anyone else see 15? Lots of connections to 15. Luke, how did you see that 15?
Luke: Because this number was just one more.
Kim: One more than what?
Luke: 14.
Kim: 1 more than 14. You saw 15, and you said, "Well earlier we had seven and seven, which was 14 and now it's just"
Luke: One more.
Kim: One more. 15 is indeed just 1 more than 14. Nice.
How did Kim help all students gain more access to the strategy of using doubles in the previous problem?
Kim referenced what students had said and restated, "Earlier we had seven and eight, so now do we just have eight plus eight," and " So, earlier we have seven plus eight and now we just have seven plus eight and one more." By bringing out the fact that students were using what they had found earlier, Kim suggests that this is a strategy worth trying.
How did Kim build the culture that students are to listen and learn from one another?
Kim asked students to repeat what other students had said or restate in their own words. Notice how she uses the natural complexity of the math to bring the disequilibrium to the forefront to talk about.
Kim: Give me a thumbs up if you agree with what Nico just said. Give me a thumbs up. Kade, can you tell me what Nico just said? I'm gonna write that down. What did he say? Did you hear him?
Kade: Um kind of.
Kim: Okay, you can ask him if you're not sure what he said. He said he saw 14 beads, did you hear how he saw it? Do you want to ask him? All the way across?
Kade: Sure.
Kim: Ask him.
Kade: Um.
Kim: You can just say, "Nico tell me again what you saw."
Kade: Tell me again what you saw.
Nico: I saw one five on the top and one five on the bottom. And that equals 10. And two whites on the top and two whites on the bottom.
Kim: Does everybody understand what Nico saw? This is your job, kids!
Class: Yeah.

BONUS: Read Kim's reflections on the lesson.
This is the transcript of the video, with bold comments of Kim reflecting on her teacher moves during the Problem String, inserted to highlight purposeful teacher moves.
Introducing the Rekenrek
- [Kim] So some of you have seen this before and you, all of you have seen this before, and you've worked with a math rack or a rekenrek before. Before we get started, can somebody tell me something that you know about this math rack, or this rekenrek? Tell me something you know. Gimme a thumbs up. Right here at your chest, when you have something that you can share. Intro thumbs as a routine for kids to share their answer.
-[Kim] Abraham, what's something you know about this thing?
- [Abraham] One side is red and one side is white and they're both…
- [Kim] What do you know about the red and white?
- [Abraham] They're both five.
- [Kim] What's five? Five red? Clarifying, labeling, establishing the 5 and 10 so we can use them later.
- [Abraham] Five red and five white.
- [Kim] Five red on top.
- [Abraham] And they both equal ten.
- [Kim] Both what? Both what equal ten? Clarifying, labeling
- [Abraham] Those, five plus five
- [Kim] Ah okay, so there's five red on top and five white on top and that equals?
- [Abraham] Ten.
- [Kim] Ten on top. Excellent. Whose got something else that they can share? Brodie, what's you got?
- [Student] Brady.
- [Kim] Brady, thank you. Brady, what you got?
- [Brady] Um, there's only 12, I mean 20.
- [Kim] 20 beads?
- [Brady] Yep.
- [Kim] On the whole thing?
- [Brady] Mm-hmm
- [Kim] How do you know? Justify. I want to know what you are thinking!
- [Brady] Cause um, there's 10 white and 10 reds.
- [Kim] Okay so there's 10 red here, and 10 white here. And all together that makes how many?
- [Class] 20!
- [Kim] Okay, excellent. Anything anybody else knows about this math rack or this rekenrek? Put your thumb up. Reinforcing thumbs. This is new to them and I'm going to encouraging it all along. Kelsey, what do you know?
- [Kelsey] Um, there's two rows on one.
- [Kim] There's a row on top and there's a row on?
- [Kelsey] Bottom.
- [Kim] How many are on top again? Cementing before we use (with kids who I think need it)
- [Kelsey] 10.
- [Kim] 10 on top. And Owen, how many are on bottom? Cementing before we use throughout the string today.
- [Owen] 10.
- [Kim] 10 on the bottom, okay. So, we all know some things about this math rack, right? Today we're gonna use our math rack to solve some problems. Are you ready?
- [Class] Ready. Yeah.
- [Kim] Okay, excellent.
Problem String
- [Kim] Okay here's what we're gonna do. I'm gonna show you some beads. I'm gonna hold my paper up and I'm gonna move some beads around and then I'm gonna show you for just a couple seconds, so you're gonna have to be ready to look, really carefully. And then I'm gonna ask you how many beads that you see. Okay, are you ready?
- [Kim}Here's your first one. Here's your first. I'm gonna show you, this right here. Are you ready to see? Focusing kids because I know it's going to be a "quick image" style problem string.
- [Class] Yes.
- [Kim] Okay. Give me a thumbs up if you can tell me how many you saw. How many you saw. Thumbs up, right here, just on your chest. Nico, what did you see?
- [Nico] 14.
- [Kim] 14 beads, and how did you see those? Important question! The arrangement he sees them in matters because I am going to record an equation.
- [Nico] I saw five red on top and five red on the bottom and two white on the top and bottom.
- [Kim] Give me a thumbs up if you agree with what Nico just said. Give me a thumbs up. Kade, can you tell me what Nico just said? I'm gonna write that down. What did he say? Did you hear him? Are students listening to each other?
- [Kade] Um kind of.
- [Kim] Okay, you can ask him if you're not sure what he said. He said he saw 14 beads, did you hear how he saw it? Do you want to ask him? All the way across? It's important to hear what people are saying.
- [Kade]Sure.
- [Kim] Ask him.
- [Kade] Um.
- [Kim] You can just say, "Nico tell me again what you saw." Supplying words to use to ask for help.
- [Kade] Tell me again what you saw.
- [Nico] I saw one five on the top and one five on the bottom. And that equals 10. And two whites on the top and two whites on the bottom.
- [Kim] Does everybody understand what Nico saw? This is your job, kids!
- [Class] Yeah.
- [Kim] Okay, awesome. Did anyone see that in a different way? You saw that there were 14, but you saw it in a different way. Sofia, what did you see? Taking variety of strategies so I can record equivalence.
- [Sofia] 10 and 4.
- [Kim] You saw it as 10 and 4, interesting. You saw those 14 as 10 and 4. What's the 10, Sofia? I wanted to be sure I knew what HER ten was. Did you see these, right here? These 10, all the reds were 10. And then you saw the four white. Can you see here, what Sophia just said? And see what she saw also? Kids, do you understand your friend's strategy? She saw 10 red beads, remember you told me that there were 10 red beads prior knowledge? And then she saw four more, so 14 can be thought of as 5 and 5 and 2 and 2 or 10 and 4. How many were on top? How many are on top? Give me thumbs up. Give me thumbs up. Reminding Kelsey, how many are on top?
- [Kelsey] Um, seven.
- [Kim] Seven, and how many are on bottom? How many are on bottom?
- [Kelsey] Seven.
- [Kim] Seven, okay. So we can see this in a couple different ways. Are you ready for the next one? We've got seven on top and seven on bottom. Establishing the double, so kids can make use of it. You ready for the next one?
- [Class] Yeah.
- [Kim] Okay, here we go. Here we go.
- [Student] I think this is gonna be hard.
- [Kim] I think you've got it. Okay, ready? Give me thumbs up. Oh, I love those thumbs. Love those thumbs. Sydney, what did you see? The important question. How they see the beads tells me what to record.
- [Sydney] 13.
- [Kim] You saw 13, and how did you see those 13?
- [Sydney] Cause I saw 10 red and 3 blues.
- [Kim] Three, how many? Three whites?
- [Sydney] Yes.
- [Kim] You saw that as 13. And you saw 10 red and 3 white. Did anyone see 10 and 3? Nice, did anyone see it in a different way? Give me a thumbs up right here. Saw it a different way. Using questions to find what I am looking for. Brady, I thought I heard you start to say something. You said it's just? Heard him say what I wanted.
- [Brady] One less.
- [Kim] One less than what? Wanted him to connect to the double.
- [Brady] 14.
- [Kim] We just had seven and seven. Which was, 14. And you said, it's just one less. So I could also say that 13 is the same as 7 plus 7 minus that 1, nice. Connecting 7+6 to 7+7.
- [Student] Whoa!
- [Kim] Really cool. Okay ready for another one?
- [Brady] It's like 13, 14, 15...
- [Kim] Ready, okay here we go. We had seven on top and seven on bottom. Then we had seven on top and six on bottom. Did I write that down? Let me write that down. We had seven on top and six on the bottom. Let's see what we're about to have. Are you ready? Here we go, ready. I love that thumb, Gemma. Luke's got... Luke's got a thumb. Abraham's got a thumb. Juliette's got a thumb. Luke's got a thumb. I wish I had NOT done this. I was publicly commenting on who was ready. That defeats the point of the private signal. Luke, what did you see?
- [Luke] 15.
- [Kim] You saw 15? Did anyone else see 15? Lots of connections to 15. Luke, how did you see that 15?
- [Luke] Because this number was just one more.
- [Kim] One more than what? Connecting problems.
- [Luke] 14.
- [Kim] 1 more than 14. You saw 15, and you said, "Well earlier we had seven and seven, which was 14 and now it's just"... Clarifying and connecting.
- [Luke] One more.
- [Kim] One more. 15 is indeed just 1 more than 14. Nice. And how many are on top?
- [Student] Uh, seven.
- [Kim] Seven, and how many are on bottom?
- [Student] Um, eight. What's the problem we did again?
- [Kim] Eight, nice. You ready for another one?
- [Class] Yeah.
- [Kim] Okay here we go. Here we go, ready? Let's see who is looking.
- [Student] Oh, I know.
- [Kim] Thumbs up. Thumbs up if you think you know.
- [Student] It's just one more.
- [Kim] Thank you. Gemma, what did you see?
- [Gemma] 16.
- [Kim] You see 16. And how did you see that 16?
- [Gemma] Just 1 more than 15.
- [Kim] You saw 16 and you said to yourself, "Self, earlier we had seven and eight, so now do we just have eight plus eight." Who heard how Gemma just solved that? She said it's just one more. Just one more than what, Juliette?
- [Juliette] 1 more than 15.
- [Kim] 1 more than 15. And how did some people see the 15?
- Student] Because...
- [Kim] Hang on. I’m trying to give wait time.
- [Juliette] There was one bead taken away from the bottom and so its just like 15. But when you add it, it's 16.
- [Kim] So, earlier we have seven plus eight and now we just have seven plus eight and one more. Okay, last one. Are you ready? Last one. Ready? I love those thumbs. Cash, what did you see?
- [Cash] 17.
- [Kim] 17, and how do you know?
- [Cash] It's because there was nine on the bottom and eight on the top.
- [Kim] Nine on the bottom and eight on top. And how do you know nine on the bottom? So I'm gonna write eight on top and nine on the bottom. And did you know that that was 17?
- [Cash] Because four plus three equals seven and if you just add 10 more to that then it's just 17.
- [Kim] Oh, who heard what he just said? He said four plus three is seven. And you add it to this 10 and that is 17. Did anyone use this problem right here that we had just done? Charlotte, you did? Can you talk to me about that?
- [Charlotte] I used it because it's kind of the same kind of the same problem except just with one more.
- [Kim] Just one more. If you already know eight plus eight, can that help you with eight plus nine? How? Cause it's just one more. Check this out. Summarize. We started off with seven and seven. And you guys said to solve seven and six, it's just one... One less. And then in order to solve seven, I'm sorry 15. You said oh that's like seven and seven and one more. Then we did eight and eight and our friend just said that 17 is like 8 and 8 and 1 more. You guys are such good thinkers. Kiss your brain.
Reflections: I would have liked for the amount of time that students were sitting for the string to be less than ten minutes, as I felt that towards the end I was losing their focus. I could have done the number rack review separately. Looking back now, I also wish that I had made a bigger deal about the doubles that were being used all throughout the string rather than just at the end when we were summarizing. Noticing and calling out the relationships explicitly can be so helpful.
